线性回归模型的模型公式一般如下：
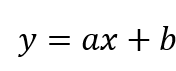
image.png
给出一组训练数据(x, y), 并采用如下的损失函数来进行训练：
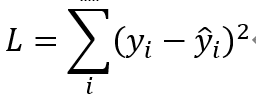
image.png

当L损失函数最小时，求得得a和b得值则是最优的。之所以选择这个损失函数，是因为当预测数据和训练数据的差最小时，得到的a和b对模型来说是最优的解，其实这是要求统计数据和预测数据的方差要尽可能地小。

但是为何是这个损失函数，为何不是如下的损失函数：
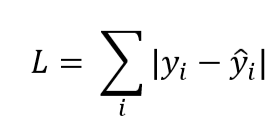
image.png
正常来说，训练数据和预测数据的差值的绝对值也可以用来描述两者之间的差距。当然可以说绝对值的函数在实数域内不是处处可导的，在数学上较难处理，但这并不是最主要的原因。
而这个主要的原因是从统计学的角度体现出来的，根据最大似然估计的方法，也可以得出这个损失函数。

我们在根据一组训练数据来求解线性回归模型的a和b时，寻找到的一条直线会尽可能地拟合训练数据，如下图所示：
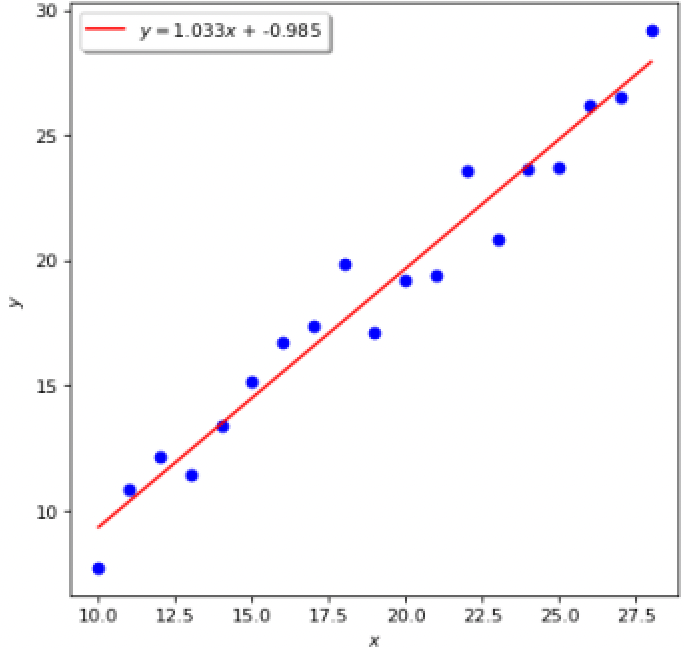
image.png

但为何这条线无法穿过所有的点呢？当然从图上来看，不可能让一条直线经过所有的点，这是显而易见的。
之所以会出现这样的原因，是因为这些点在满足y=ax+b的基础上，还有一个随机扰动，这个随机扰动干扰了我们获得y=ax+b这个数据的内在规律，否则如果没有这个随机扰动，这些训练点就会完全满足y=ax+b这个公式，所有的点都会落在这条线上。如果是这样，就不需要做什么机器学习了，直接用数学公式建模不就好了？哪里还需要这些训练数据，正常两个点就能确定这么一条直线。

所以机器学习中的线性回归模型的内在目标，是要在训练集满足y=ax+b+c（为随机扰动项）的情况下，尽可能根据训练数据，来获取真正的知识：y=ax+b，尽可能排除这个随机扰动项对我们寻找内在规律的干扰。这才是线性回归模型作为机器学习的本质。

上面说了这么多，终于让我认识到实际的训练数据集满足的并不是y=ax+b这个确定的规律，而是满足y=ax+b+c这个规律，而这个c则是随机的扰动项，就像在真实世界收集的数据，总是会有各种各样的误差一样，这个随机扰动总是存在的。
从数学上来讲，c这种在物理世界中存在的随机扰动项，它的分布规律是服从正态分布的，那么y=ax+b+c其实也是服从正态分布的。

如果要拟合出来一条直线，让所有的y都能尽可能地满足这条直线，就要求所有y的概率的乘积为最大。为了解释这句话，我们可以简单的用概率论中的知识来举例，比如第一个点的概率假设是P，第二个点的概率是Q，那么这两个点都存在的概率就是PQ，如果第三个点地概率假设是S，那么三个点都存在地概率就是PQ*S。这就是乘积地由来，因为我们是在拟合直线，所以要求所有点地概率乘积为最大，而这个乘积函数，就是所谓地似然函数。即：
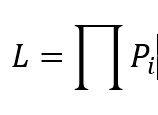
image.png

最大似然估计，也就是要求这个似然函数最大的时候，我们得到的那条拟合函数。前面说到y=ax+b+c是符合正态分布的，那么我们就可以根据正态分布得到每一个点的概率：
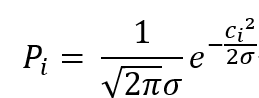
image.png

我们知道y=ax+b+c,所以可以知道：
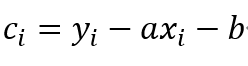
image.png

带入每个点的概率公式，得到：
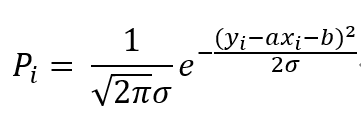
image.png

因为似然函数是各个点的概率的乘积，而这里又有指数函数，可以使用对数函数，将乘法转换为加法，则：
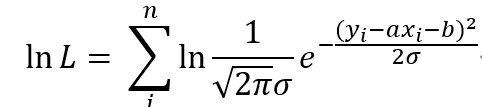
image.png

变换一下，就可以得到：
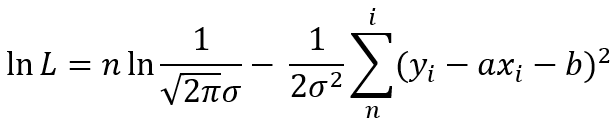
image.png

前面这一项是个常数，如果要L最大，那么就需要后面这一项最小，所以就要求
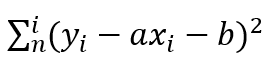
image.png
最小。
如果我们获得了一个拟合模型，将x带入拟合的模型，得到的预测值就是：
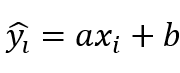
image.png

所以从最大似然估计的角度，最后得到的损失函数也是：
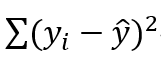
image.png

综上，从方差和最大似然估计，得到了相同地损失函数。这也是为何不选择绝对值样式地损失函数地原因。当然，这里并不是说绝对值方式地损失函数不行，其实在减少异常数据干扰地能力上，绝对值损失函数要比平方损失函数要更强一些。

下面贴上使用python训练一个线性回归模型地代码：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Thu Apr 21 22:37:23 2022
此脚本用于随机生成线性回归模型的训练数据
@author: zhoutingyu
"""

import os
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

def generate_data():
    """
    随机生成数据

    Returns
    -------
    None.

    """
    # 规定随机数生成的种子
    np.random.seed(4888)
    x = np.array(list(range(10, 29)))
    error = np.random.randn(19)
    y = x + error
    return pd.DataFrame({"x": x, "y": y})


def visualize_data(data):
    """
    数据可视化

    Parameters
    ----------
    data : TYPE
        DESCRIPTION.

    Returns
    -------
    None.

    """
    fig = plt.figure(figsize=(6,6), dpi=80)
    ax = fig.add_subplot(111)
    
    ax.set_xlabel("$x$")
    ax.set_xticks(range(10, 31, 5))
    ax.set_ylabel("$y$")
    ax.set_yticks(range(10, 31, 5))
    
    ax.scatter(data.x, data.y, color="b", label="$y = x + \epsilon$")
    plt.legend(shadow=True)
    
    plt.show()
    
if __name__ == "__main__":
    data = generate_data()
    home_path = os.path.dirname(os.path.abspath(__file__))
    if os.name == "nt":
        data.to_csv("%s\\simple_example.csv" % home_path, index=False)
    else:
        data.to_csv("%s/simple_example.csv" % home_path, index=False)
    visualize_data(data)

效果：
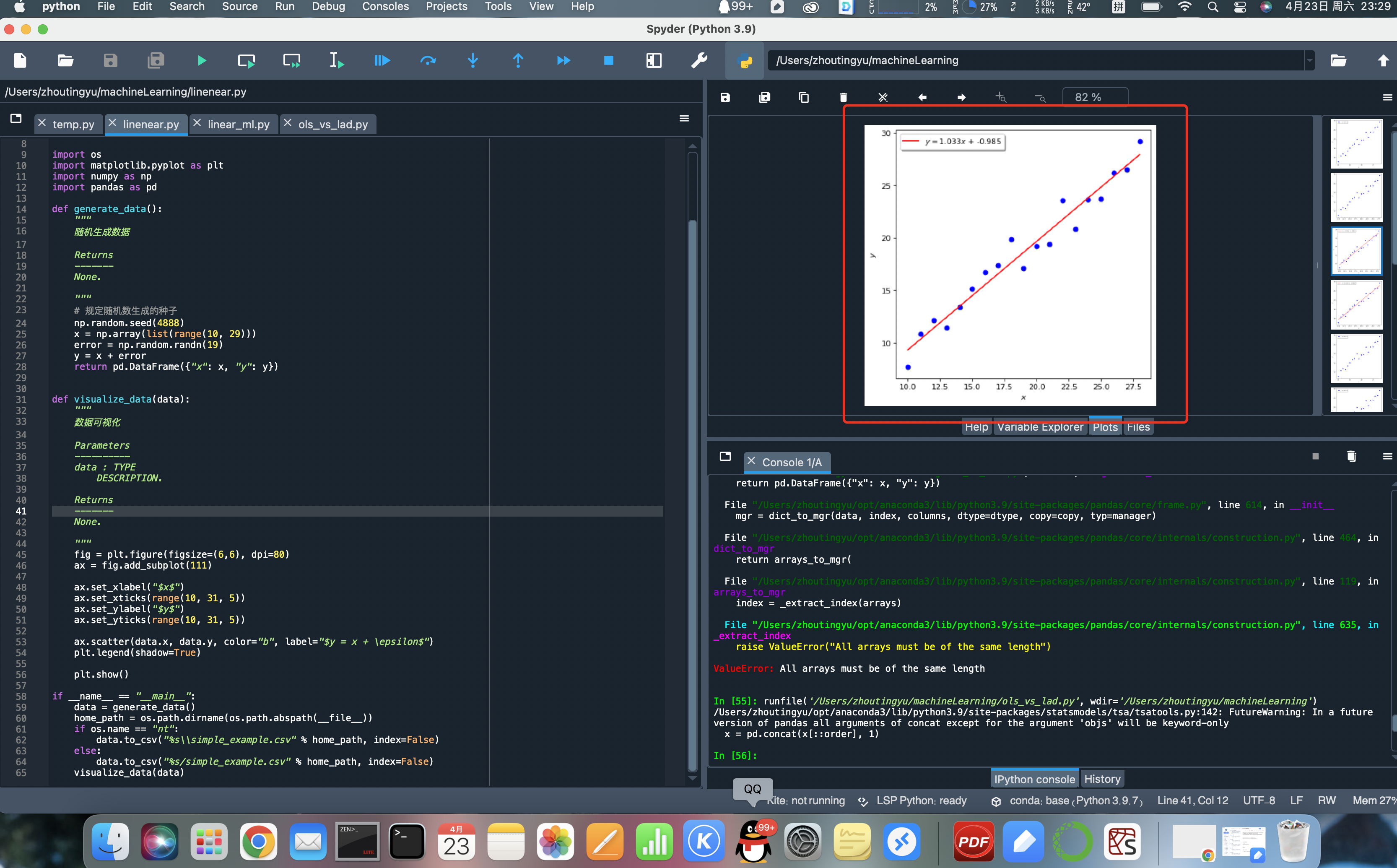
image.png

Q.E.D.